Imagine reading two different abstracts. Both study the same effect. Both use the same methods and stimuli. Both have the same high subject count (N). One reports an effect size of d = 0.1 [-0.2, 0.4] (p = 0.3). The other reports an effect size of d = 3.0 [2.0, 4.0] (p = 0.0003).

These vastly different outcomes could easily occur due to differing experiment and analysis approaches that almost never appear in the abstract. No statistical fluke needed. In fact, direct replications would likely yield very similar results.

Studies are often complimented and criticized based on the sample size (N) and standardized effect size (Cohen’s d). “That N is too small for me to trust the results“. “That Cohen’s d is impossibly large“. But when there are within-subject designs or replicate trials, N and Cohen’s d don’t reliably inform about statistical power or reliability. The simple parameters that often appear in abstracts are so vague and uninterpretable that any heuristic based on them is necessarily flawed.

Subject count is only one dimension of sample size

Let’s establish some terminology to avoid confusion. Here are definitions as I use them:

• Between-subjects: Each subject runs in one condition
• Within-subjects: Each subject runs in every condition (a.k.a. “repeated measures”)
• Replicate trials: How many times each subject runs in the same condition

So if an experiment with 2 conditions has N=10, is between-subjects (5 per condition), and each subject performs their condition 1 time, then there are (5 + 5 subjects) × (1 condition each) × (1 replicate trial)  = 10 total samples.

But if an experiment with 2 conditions has N=10, is within-subjects, and has 20 replicate trials, then there are (10 subjects) × (2 conditions each) × (20 replicate trials) = 400 total samples.

Both could be labelled as “N=10” despite the 40x difference in sample count. And that’s not to mention that within-subjects data factors out some of the noise from individual differences, making the experiment more sensitive.

Effect size and Cohen’s d

Cohen’s d is the difference between conditions divided by the standard deviation (mean(a) - mean(b)) / sd(all). For between-subjects experiments without replicate trials, there is little ambiguity. But for data that is within-subjects or has replicate trials, difference and standard deviation of WHAT? How you aggregate can massively impact standard effect sizes, and most papers don’t differentiate which definition they’re using.

Jake Westfall has a great post on five possible definitions of Cohen’s d for within-subjects designs, so there’s no need to rehash all them. Here, I’ll focus on the three I see frequently used:

d_a – Average over the replicate trials for each subject and then run a classic Cohen’s d. Importantly, this approach is inappropriate for within-subjects data because measures from the same subject are not independent.

d_z – Average over the replicate trials for each subject in each condition, then compute the difference between conditions for each subject, and divide the average of the differences by the standard deviation of the differences.

d_r – Use the variance of all residuals, including individual replicate trials, in computing the standard deviation. See (Brysbaert & Stevens 2018).

Simulation

To see how replicate trials counts and Cohen’s d definitions impact the resulting effect size, I ran a simulation of a simple experiment partly based on some actual data:

• Two conditions: A and B
• A normally distributed continuous response
• Condition B has responses 0.1 higher than condition A (the “true” effect)
• Normally distributed individual differences in the baseline (sd = 0.2)
• Normally distributed response noise (sd = 0.5)

The formula for a response is:

response = subject_baseline + 0.1*(condition == B) + trial_response_noise

I varied:

• Number of subjects (10, 40)
• Replicate trial count (1, 5, 25, 125, 625)
• Within-subjects vs. between-subjects and Cohen’s d definition
  (da between, dr between, dz within, dr within)

For each combination, I ran the simulation 5000 times, and plotted the distribution of the resulting effect sizes. Here is the code.

Results

Here are two different visualizations of the effect sizes from each simulated scenario:

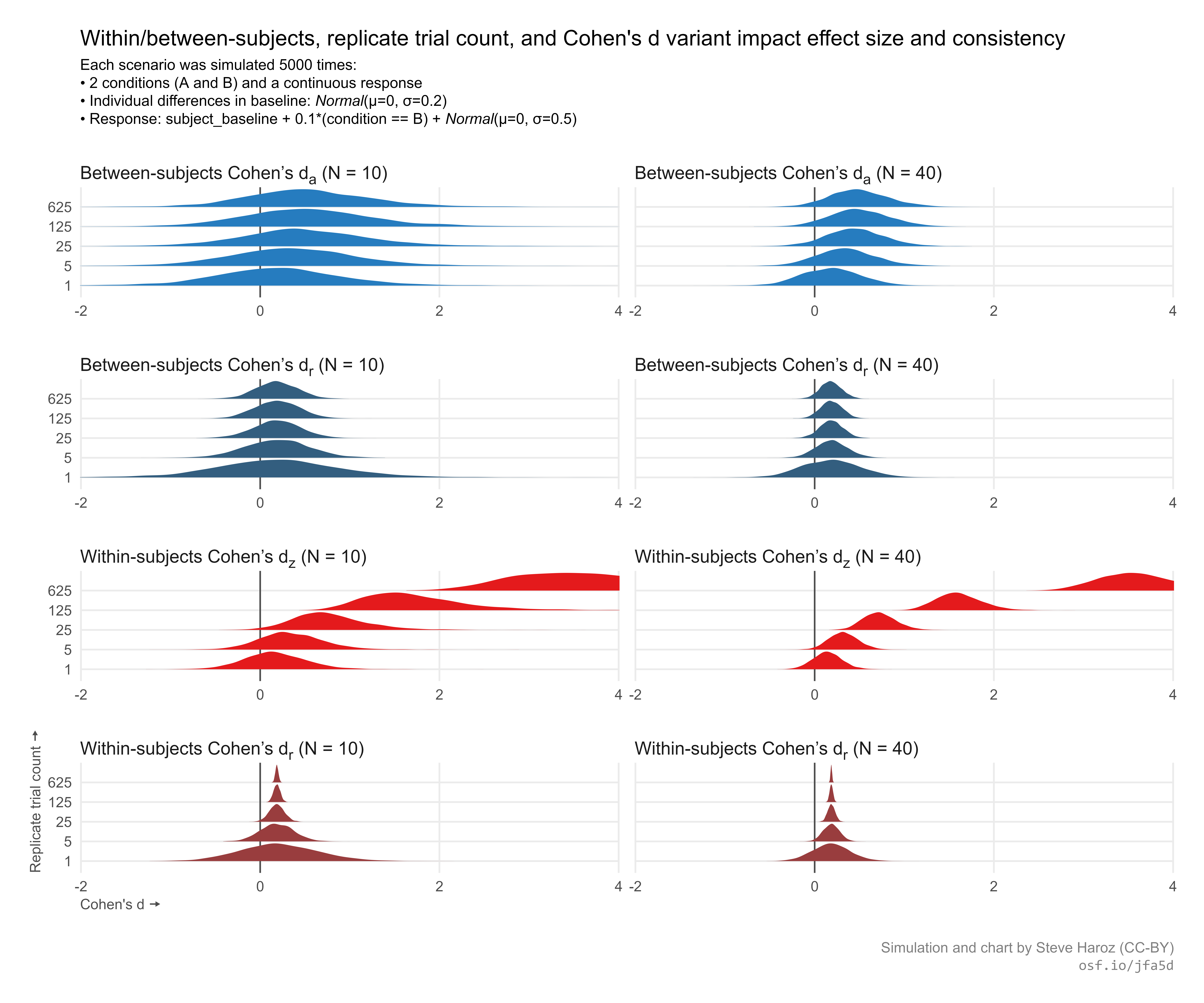
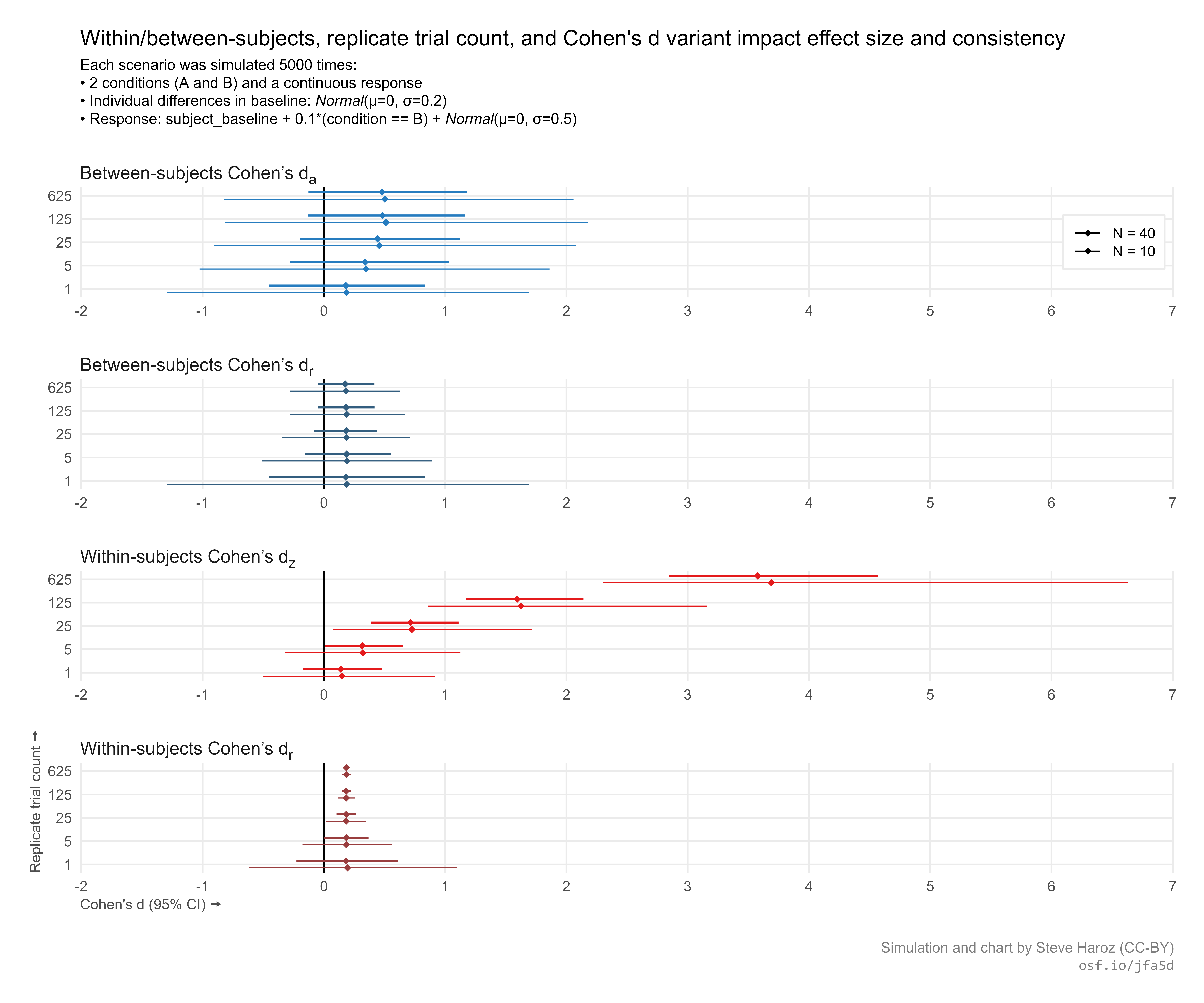
Between-subjects experiments are much less sensitive. None of the between-subjects scenarios reliably show an effect. The centers of the distributions are all positive, but they all have a sizable proportion of the simulations yielding negative effect sizes. The replicate count and Cohen’s d definition don’t seem to matter much. A much higher N would be needed to reliably get a positive effect size.

For within-subjects d_z, higher replicate trial counts yield a much larger effect size. The 625 replicate condition even had to be cropped to keep the scale reasonable. The reason is that this approach “cancels out” two sources of noise. The within-subjects design accounts for individual differences. And averaging replicate trials accounts for response noise. So you end up dividing the mean by a negligeable standard deviation, producing a very large effect size.

For within-subjects d_r, higher replicate trial counts yield a much more consistent effect size. The 125 and 625 replicate counts produced effect sizes that were practically identical across all 5000 simulations.

Take-aways

Cohen’s d is too ambiguous to be reported without clarification. Clarifying the formula used to calculate effect size should be expected, just like it’s expected to report the analysis type and degrees of freedom when reporting p-values. I’m also worried about meta-analyses naively combining different types of effect sizes thinking they’re all the same.

N is only one parameter of statistical power, and it’s not always the most important. I think of statistical power like the volume of a box: Having only one dimension’s measurement isn’t very useful for computing the volume. Likewise, only reporting N in an abstract isn’t very informative. Let’s stop putting N in abstracts, and only report it in the methods section where it has context.

Naive heuristics. A lot of reviewers and even journalists unfortunately rely on simple heuristics that only make use of the N. Consequently, many researchers that use lots of replicate trials to get more sensitive experiments have had negative experiences with a general psychology journal rejecting their work “because the N is too small”. If offered the choice between a cubic inch of gold or a 10 inch long sheet of gold leaf, these reviewers would choose the gold leaf because they’re only considering length.

Goodhart’s law: The heuristic becomes the target. A consequence of simplistic reporting and naive heuristics may be that we are incentivizing less sensitive experiments and less reliable results. If a researcher has a fixed budget, and they can either run (a) 10 subjects with 100 trials each or (b) 1000 subjects with 1 trial each, which result is going to be easier to get published? Probably (b), even though (a) may be more accurate and precise when there is a lot of noise from individual differences in baseline and high response noise.

Careful dismissing “impossibly large effect sizes”. With lots of replicate trials, Cohen’s d_z can become enormous. I don’t think it’s necessarily “wrong”, but it’s not comparable to any measure of Cohen’s d from a different experiment design. An alternative that I typically see is to use partial eta squared (η_p²) (Richard Morey has a good explanation), but I’m not sure that’d help with interpretability. And I’m not sure that d_r is much better.

Is Cohen’s d_r the best option? Not necessarily. Jeff Rouder has a great post on this issue where he points out that within-subjects experiment designs are much better at separating different sources of noise, but d_r smashes all those sources of noise together. I think it’s necessary to end any statistical discussion by stating that what’s most important in any effect size is the appropriateness of the model in accounting for all the sources of variability.

---

This post is part 1 of a series on statistical power and methodological errors. See also:

More precise measures increase standardized effect sizes

Invalid Conclusions Built on Statistical Errors