My last post – Simulating how replicate trial count impacts Cohen’s d effect size – focused mostly on how parameters of within-subjects experiments impact effect size. Here, I’ll clarify how measurement precision in between-subjects experiments can substantially influence standardized effect sizes.
More replicate trials = better precision
A precise measurement is always an aim of an experiment, although practical and budgetary limitations often get in the way. Attentive subjects, carefully calibrated equipment, and a well controlled environment can all improve measurement precision. Averaging together many replicate trials is another approach for improving precision, and it can also be easily simulated.
To show that replicate trial count is a proxy for precision, I ran a simulation that varied the number of replicate trials. For each subject, I sampled 100 measurements from a normal distribution. Then I used either (a) just the first measurement, (b) the average of the first 10 measurements, or (c) the average of all 100 measurements as that subject’s overall measurement. With more replicate trials, the variability of the overall measure reduces. More replicate trials = better precision.
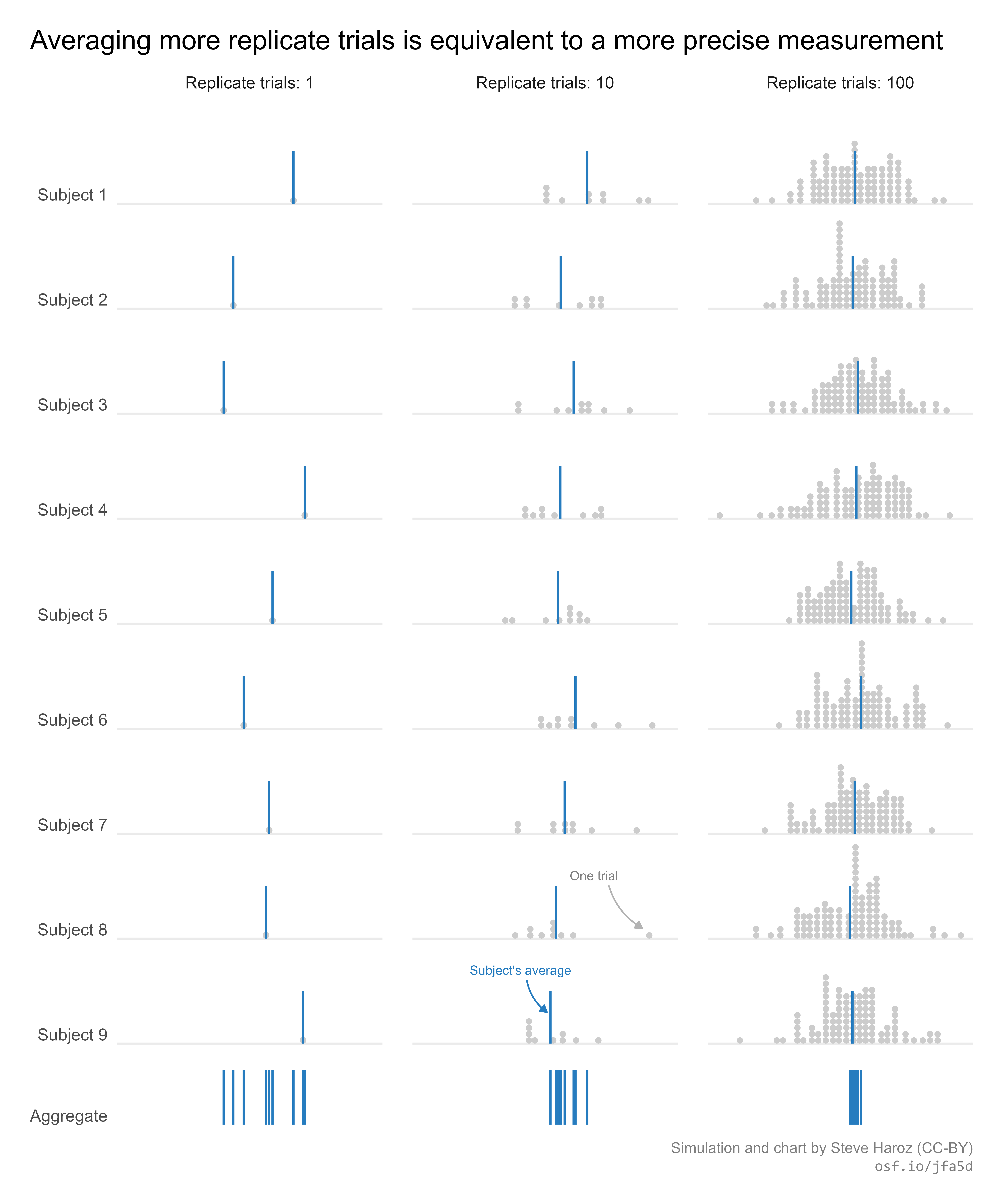
Notice that the blue lines are much more tightly packed with 100 replicate trials than with 10 or 1.
Simulating the same effect with different measurement precision
To see the impact of increasing precision, I ran a simulation:
- Two conditions: A and B
- A normally distributed continuous response
- Condition B has responses 0.2 higher than condition A (the “true” effect)
- Normally distributed individual differences in the baseline (sd = 0.1)
- Normally distributed response noise (sd = 1)
The formula for a response is:
response = subject_baseline + 0.2*(condition == B) + trial_response_noise
For each replicate trial count (1, 5, 25, 125, 625, and 3125), I ran 5000 simulations and plotted the distribution of Cohen’s da, which is the classic formula for Cohen’s d based on subject means. Here is the code.
Results
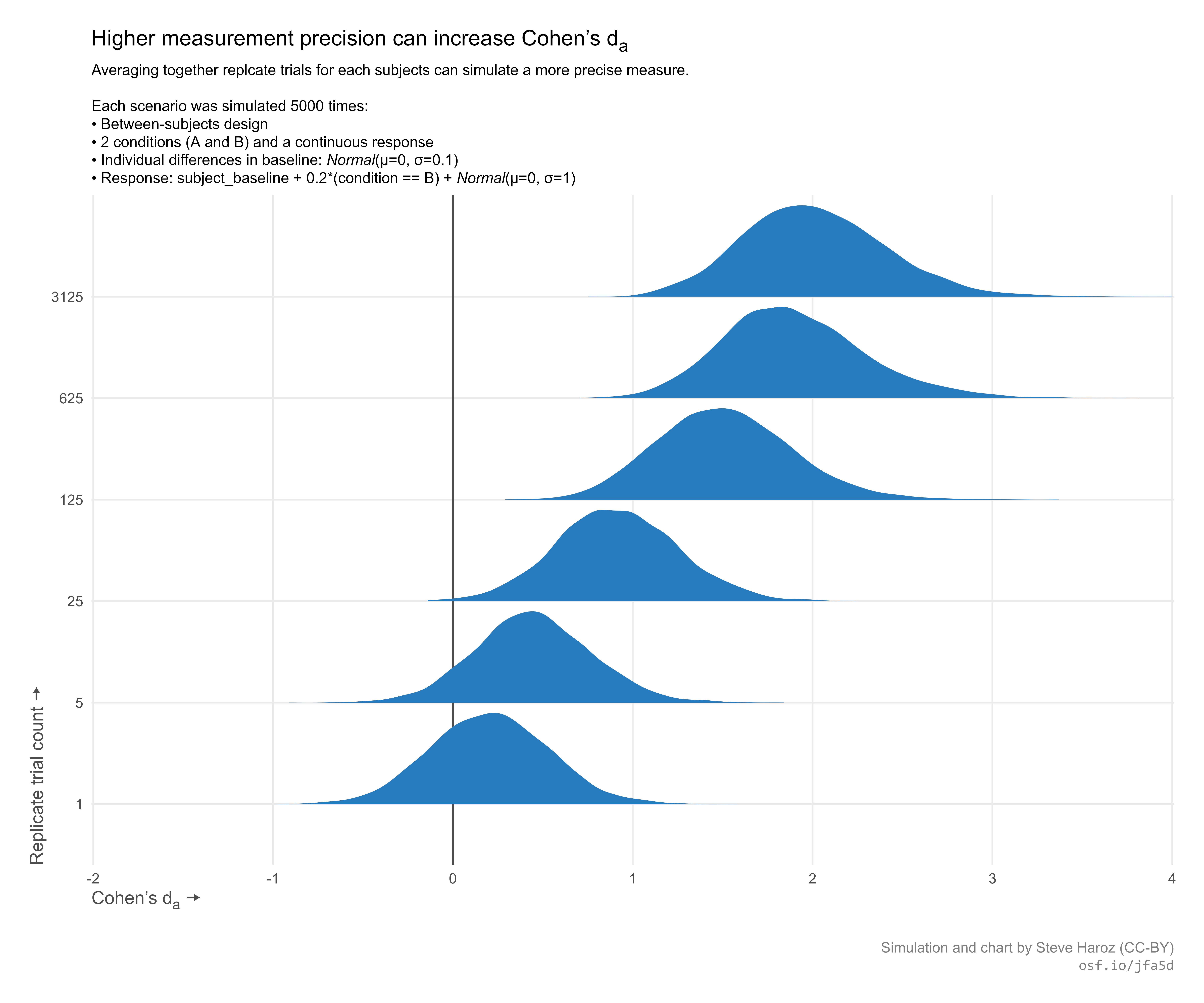
The exact same effect measured under different between-subject experiments yields a different effect size. As the replicate trial count (measurement precision) increase, the effect size increases.
The reason is that increasing the measurement precision, reduces the standard deviation. Since Cohen’s d is (mean(a) - mean(b)) / sd(all), and the standard deviation is in denominator, higher precision results in a lower standard deviation, which results in a lower standardized effect size.
Be careful comparing effect sizes across experiments
Measurement precision can be impacted by many factors that are often tough to pin down. So it’s worth having a certain degree of skepticism when interpreting nominal effect size values or comparing them across experiments. Even when experiments test the same effect, differences in precision can yield very different standardized effect sizes.
The sensitivity to precision raises concerns about the validity of some meta-analyses. If all of the experiments in a meta-analysis are carefully performed direct replications, then precision should be similar and the results can be pooled. But I don’t see how indirect replications or unrelated studies on a similar phenomenon can be used in a meta-analysis. Any difference in experiment design could change the precision, yielding subtly or wildly different standardized effect sizes.
If the simulated precision levels above were each different experiments in a meta-analysis, it’d be tough to draw a conclusion due to the high variance. And if one were a replication of another, there could be drama due to the order of magnitude difference in effect sizes. So keep that in mind when judging replicability using effect size value or a meta-analysis with high variance between experiments.
Takeaways
Standardized effect size values have little meaning outside of a specific experiment. Effect size is a function of the experiment design and analysis approach. So describing an effect outside of the context of the experiment just isn’t meaningful.
Small, medium, and large are not meaningful categories. If the nominal value can vary with the experiment design, then arbitrary demarcations of categories doesn’t add any practical clarity for anyone.
Focus on uncertainty instead of point estimates. 95% confidence intervals of an effect size are much more interesting to me than an estimate of a specific value. An effect size with a 95% CI of [0.4, 0.6] is much more interesting to me than an effect size with a 95% CI of [-1, 3].
Thanks to Aaron Caldwell and Matthew B Jané for helpful comments.
This post is part 2 of a series on statistical power and methodological errors. See also:
Simulating how replicate trial count impacts Cohen’s d effect size

Are there any bias-correction techniques in the meta-analysis community for this? I’m against meta-analyzing results without strong and comparable methods too, but wonder if some statistician has explored this problem.
Not that I know of. In general, aggregating similar measures (e.g., direct replications) will reduce noise but not bias.
Yes there is. So if you know the average inter-trial correlations and you know the number of trials. You can obtain the reliability via spearman-brown prophecy formula:
rXX = k*r_trials / (1 + (k – 1)*r_trials)
Using the estimated reliability, you can correct for bias by dividing the standardized mean difference by the square root of the reliabilities in X and Y
For Cohen’s d: d(corrected) = d / sqrt(rYY)
For Pearson Correlation: r(corrected) = r / sqrt(rXX*rYY)
The correction will also need to be applied to the standard error as well.
You can find these equations in Hunter and Schmidt’s textbook “meta-analysis methods” or in the fantastic paper by Brenton Wiernik: https://journals.sagepub.com/doi/full/10.1177/2515245919885611
Thanks for this great post! The pitfalls of all these standardised effect sizes are really not sufficiently well known. This also impacts power analyses for planning new experiments. We regularly encounter this as editors in the Registered Reports team because people will suggest an effect size of interest based on previous studies even when none of the experimental parameters are even remotely matched. I typically suggest to authors to use a principled approach for the raw effect size of interest and then base power analysis on the relative effect size that this can yield given their experimental design. But most people struggle with that as there is no one size fits all solution.
Yeah, using results from one study to inform the sample size of another is only straight forward for direct replications. I’ve wondered if stage 2 for registered reports should reconfigured to have the authors take the approved experiment paradigm and data-peek/p-hack their way through data collection until they get a result that meets some threshold. Then stage 3 is a direct replication of the sample size and exclusion criteria that stage 2 ended up using.
This is a good idea – in a way not dissimilar to how I envisioned Exploratory Reports to work. You’d do an ER first and then a RR to replicate the findings and then the two would constitute a larger unit but each can be published in their own right. That’s not quite the same because your proposal would involve some preregistered and reviewed component for the Stage 1-2 already – but I think that would generally be a good idea too. Many studies would benefit from being reviewed before data collection commences. (It also generally makes the review process much more pleasant because it’s no longer a fight but a collaboration between authors and reviewers).